Hubble-Parameter

Nicht maßstäblich, nur zur Illustration:
Entwicklungsstadien des Universums

Maßstabsgetreu:
Zeitliche Entwicklung der Ausdehnung und Horizonte des Universums

Die Hubble-Konstante $LaTeX: H_0$, benannt nach dem US-amerikanischen Astronomen Edwin Hubble, ist eine der fundamentalen Größen der Kosmologie. Sie beschreibt die gegenwärtige Rate der Expansion des Universums. Mittlerweile wird auch häufig der Begriff Hubble-Parameter verwendet, da die Hubble-Konstante genau genommen keine Konstante ist, sondern sich mit der Zeit verändert. Der homogene Vorgang der Expansion wird als Hubble-Fluss oder Hubble Flow bezeichnet.

Die Messung der Hubble-Konstante erfolgt über die systematische Erfassung der Entfernung und der scheinbaren Geschwindigkeit von astronomischen Objekten in Bezug auf uns. Da es sich dabei um weit entfernte astronomische Objekte handeln muss, sind die Messungen aufwändig und mit im Vergleich zu anderen Naturkonstanten großen Unsicherheiten behaftet. Dazu kommt, dass die Hubble-Konstante, anders als der Name andeutet, im Laufe der Zeit ihren Wert geändert hat. Messungen zu Beginn des 21. Jahrhunderts ergaben Werte zwischen $LaTeX: 68 \ \tfrac{\mathrm{km}}{\mathrm{s \cdot Mpc}}$ und $LaTeX: 74 \ \tfrac{\mathrm{km}}{\mathrm{s \cdot Mpc}}$.

Definition

Die Expansion des Universums wird quantitativ beschrieben durch den Skalenfaktor $LaTeX: a (t)$, dessen zeitliche Entwicklung als Lösung der Friedmann-Gleichungen der relativistischen Kosmologie gegeben ist. Der zeitabhängige Hubble-Parameter beschreibt die Expansionsrate und ist definiert durch

$LaTeX: H(t) = \frac{\dot a(t)}{a(t)},$

wobei $LaTeX: \dot a(t)$ die zeitliche Ableitung des Skalenfaktors ist.

Der heutige Wert des Hubble-Parameters wird als Hubble-Konstante $LaTeX: H_0$ bezeichnet:

$LaTeX: H_0 = H(t_0)$

mit dem Weltalter $LaTeX: t_0$. Der gemessene Wert der Hubble-Konstante liefert die notwendige Anfangsbedingung zur Lösung der Friedmann-Gleichungen.

Im lokalen Universum (also über Entfernungen, die klein sind im Vergleich zum Radius des beobachtbaren Universums) ist die Hubble-Konstante die Proportionalitätskonstante der (näherungsweise) linearen Beziehung zwischen den Entfernungen $LaTeX: D$ von Galaxien und den aus ihren Spektren gemessenen Rotverschiebungen $LaTeX: z$:

$LaTeX: c \cdot z \approx H_0 \cdot D.$

Dabei ist $LaTeX: c$ die Lichtgeschwindigkeit.

Häufig wird das Produkt $LaTeX: c \cdot z$ im Sinne des Dopplereffekts als Rezessionsgeschwindigkeit $LaTeX: v$ interpretiert, man erhält dann

$LaTeX: \Leftrightarrow v \approx H_0 \cdot D.$

Die genaue Beziehung zwischen kosmologischer Rotverschiebung und Entfernung ist nichtlinear und erfordert eine Integration über den zeitlichen Verlauf des Skalenfaktors $LaTeX: a (t)$.

Erste Messungen Edwin Hubbles ergaben für die Hubble-Konstante $LaTeX: H_0$ in SI-Einheiten einen um den Faktor 7,446 zu hohen Wert von 1,6·10⁻¹⁷ s⁻¹. Zumeist wählt man jedoch eine traditionelle Einheit und erhält dann 500 km s⁻¹ Mpc⁻¹. Dieser Zahlenwert ist so zu verstehen: Man beobachtet zwei Galaxien A und B und misst ihre Spektrallinien. Unterscheiden sich die Wellenlängen so, dass sich für die Galaxie A mit den heute aktuellen Werten ein um 67,74 km/s höherer Wert $LaTeX: c \cdot z$ ergibt als für B, so sollte die Galaxie A etwa 1 Mpc (reichlich drei Millionen Lichtjahre) weiter entfernt sein als die Galaxie B.

Da Galaxien nicht nur der kosmischen Expansion folgen, sondern zusätzlich eigene Bewegungen von typisch einigen hundert km/s zeigen, müssen viele Galaxien über einen genügend großen Entfernungsbereich untersucht werden, um beide Effekte zu trennen. Die durch die kosmische Expansion bedingte „Geschwindigkeit“ $LaTeX: c \cdot z$ und die kosmologische Rotverschiebung haben einen anderen Ursprung als eine Eigengeschwindigkeit und die mit ihr durch den Dopplereffekt verbundene Rot- oder Blauverschiebung.

Hubble-Diagramm

Die Auftragung der Rotverschiebung von astronomischen Objekten gegen ihre Entfernung von der Erde wird Hubble-Diagramm genannt. Ein sich gleichmäßig ausdehnendes Universum führt dazu, dass die Objekte in diesem Diagramm entlang einer durch den Ursprung führenden Geraden angeordnet sind. Die Steigung dieser Geraden ist die Hubble-Konstante.

Das erste Hubble-Diagramm wurde 1929 von Edwin Hubble veröffentlicht. In dieser Veröffentlichung berichtete er von einem linearen Zusammenhang zwischen der Entfernung von Galaxien (extragalactic nebula) und ihrer Rotverschiebung. Die Bestimmung des Abstands eines weit entfernten astronomischen Objekts ohne Rückgriff auf die Rotverschiebung erfolgt aus der Helligkeit von Standardkerzen. Das Bild des Objekts muss dazu so gut aufgelöst sein, dass kein Licht anderer Objekte das Messergebnis verfälscht. Dies wird mit zunehmender Entfernung immer schwieriger. Die im ersten Hubble-Diagramm verwendeten Daten reichten bis zu einem Abstand von etwa 2 Mpc. Knapp ein Jahrhundert später sind Messungen bis etwa 700 Mpc möglich. Dadurch ist eine erheblich zuverlässigere Angabe der Hubble-Konstante möglich.

Messungen

Hubble-Konstante mit Fehlertoleranz über Messverfahren bzw. -instrumente: 1. Hubble-Weltraumteleskop, 2. Raumsonde WMAP, 3. Gravitationslinseneffekt

Spitzer-Weltraumteleskop

Unter Verwendung von Daten des Spitzer-Weltraumteleskops, basierend auf Beobachtungen im 3,6-μm-Bereich (mittleres Infrarot) zur Neukalibrierung der Cepheiden-Distanzskala, erhielten die Wissenschaftler des Carnegie Hubble Programs neue, hochgenaue Werte für die Hubble-Konstante. Dadurch konnte dieser nun um einen Faktor 3 genauer bestimmt werden. Damit hat die Hubble-Konstante nur noch eine Unsicherheit von drei Prozent (Stand 16. August 2012):

$LaTeX: H_0 \approx (74{,}3 \pm 2{,}1) \ \frac{\mathrm{km}}{\mathrm{s \cdot Mpc}}$

Hubble-Weltraumteleskop

Das Hubble-Weltraumteleskop ist in der Lage, mit Hilfe einer Entfernungsskala Entfernungen im Universum und damit auch die Expansionsrate des Universums zu ermitteln. Als Indikatoren dazu dienen Cepheiden (pulsierende Sterne mit einem Zusammenhang zwischen Periode und maximaler Leuchtkraft) und Supernovae vom Typ Ia (Standardkerzen).

$LaTeX: H_0 \approx (74{,}2 \pm 3{,}6) \ \frac{\mathrm{km}}{\mathrm{s \cdot Mpc}}$

Gravitationslinseneffekt

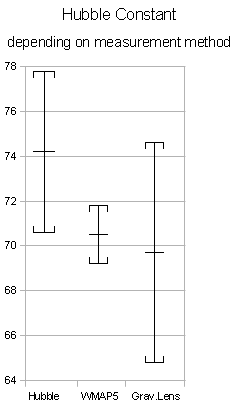
Eine vergleichsweise neue Methode macht sich den Gravitationslinseneffekt zunutze. Dabei werden Helligkeitsschwankungen um eine Gravitationslinse ausgewertet. Das Licht einer Quellgalaxie wird durch eine davorliegende Galaxie abgelenkt, wodurch sich mehrere Abbilder der Quelle ergeben. Ändert sich nun die Helligkeit der Quellgalaxie, so macht sich dies zu unterschiedlichen Zeiten in den verschiedenen Abbildern bemerkbar. Aus dem Zeitunterschied lässt sich dann die absolute Entfernung berechnen. Aus der ermittelten Entfernung und der Rotverschiebung als Maß für die Geschwindigkeit, mit der sich Objekte von uns wegbewegen, lässt sich die Expansionsrate des Universums bestimmen. Die Auswertung von Hubble-Bildern nach der Gravitationslinsen-Methode ergibt:

$LaTeX: H_0 \approx (69{,}7 \pm 4{,}9) \ \frac{\mathrm{km}}{\mathrm{s \cdot Mpc}}$

WMAP

Die Raumsonde WMAP bedient sich der Temperaturverteilung der elektromagnetischen Strahlung im Mikrowellenbereich. Einen Teil dieser Mikrowellenstrahlung liefert die kosmische Hintergrundstrahlung, die auf den Urknall zurückgeführt wird. Man misst extrem geringe Temperaturschwankungen (Anisotropien), die durch Streuung der Strahlung an den ersten Urgalaxien verursacht wurden und deren Muster bis heute erhalten sind. Aus fünf Jahren Messungen mit WMAP (WMAP5 genannt) ergibt sich:

$LaTeX: H_0 \approx (70{,}5 \pm 1{,}3) \ \frac{\mathrm{km}}{\mathrm{s \cdot Mpc}}$

Weltraumteleskop Chandra

Messungen mit dem Weltraumteleskop Chandra ergaben:

$LaTeX: H_0 \approx (77 \pm 4) \ \frac{\mathrm{km}}{\mathrm{s \cdot Mpc}}$

Supernovae und Cepheiden

Eine Entfernungs- und Geschwindigkeitsmessung von 261 Typ-Ia Supernovae und 600 Cepheiden ergab:

$LaTeX: H_0 \approx (73{,}8 \pm 2{,}4) \ \frac{\mathrm{km}}{\mathrm{s \cdot Mpc}}$

Planck-Weltraumteleskop

Messungen des Planck-Weltraumteleskops der ESA ergaben:

$LaTeX: H_0 \approx (67{,}74 \pm 0{,}46) \ \frac{\mathrm{km}}{\mathrm{s \cdot Mpc}}$

Hubble-Zeit

Der Kehrwert 1/H₀ der Hubblekonstante wird Hubble-Zeit genannt. Bei gleichförmiger Expansion in einem leeren Universum wäre sie gleich dem Weltalter, d. h. der seit dem Urknall vergangenen Zeit.

Das Verhältnis von Weltalter und Hubble-Zeit, dargestellt als Funktion der Anteile von Materie und Dunkler Energie an der Gesamtdichte des Universums.
Die zwei markierten Zustände sind im Text erläutert.

Je nach dem Gehalt des Universums an normaler (baryonischer) Materie, Dunkler Materie und Dunkler Energie kann die Expansion aber verzögert oder beschleunigt werden, so dass sich das Weltalter von der Hubble-Zeit unterscheidet:

$LaTeX: t_0 = \frac{1}{H_0} \cdot F(\Omega_m, \Omega_\Lambda, \dots)$

durch einen Korrekturterm F

$LaTeX: \Leftrightarrow F(\Omega_m, \Omega_\Lambda, \dots) = \int_0^a \frac{{\rm d}a'}{\sqrt{\Omega_r/a'^2+\Omega_m/a'+\Omega_k+\Omega_{\Lambda} \ a'^2}}$

der u. a. abhängt von den Dichteparametern

• $LaTeX: \Omega_r$ der Strahlungsdichte,
• $LaTeX: \Omega_m$ der gesamten Materie (normale baryonische und Dunkle Materie, vgl. Lambda-CDM-Modell),
• $LaTeX: \Omega_\Lambda$ der Dunklen Energie (s. auch kosmologische Konstante) und
• $LaTeX: \Omega_k$ dem Krümmungsparameter.

Z. B. wäre für lange diskutierte kosmologische Modelle mit flacher Geometrie ($LaTeX: \Omega_m + \Omega_\Lambda = 1$) und ohne dunkle Energie ($LaTeX: \Omega_\Lambda = 0 \Rightarrow \Omega_m = 1$) das Weltalter geringer als die Hubble-Zeit (vgl. Abbildung):

$LaTeX: F = 2/3 \approx 0{,}667 \Rightarrow t_0 \approx 8{,}9 \, \mathrm{Mrd. \, Jahre}.$

Mit den heutigen Messungen des Planck-Weltraumteleskops

$LaTeX: H_0 = 67{,}15~{\mathrm{km}}/{\mathrm{s / Mpc}}, \; \Omega_m = 0{,}315,\; \Omega_r = 5{,}5\cdot 10^{-5}, \; \Omega_k<0{,}005, \; \Omega_\Lambda = 1-\Omega_m-\Omega_r+\Omega_k$

ergibt sich eine Hubble-Zeit von

$LaTeX: \frac{1}{H_0} = 14{,}561 \, \mathrm{Mrd. \, Jahren},$

also ein um den Korrekturfaktor $LaTeX: F=1{,}0517$ höherer Wert als das tatsächliche Weltalter

$LaTeX: t_0 = \int_0^{a_0} \frac{1}{a\cdot H(a)} \, \text{d}a \approx \frac{2 \operatorname{arsinh} \sqrt{{a_0}^3 \Omega_{\Lambda} / \Omega_m}}{3 H_0 \sqrt{\Omega_{\Lambda} }}\approx 13{,}844 \, \mathrm{Mrd. \, Jahren}$

mit $LaTeX: a_0 = \frac{\rm 1m}{\rm 1m}=1$ und

$LaTeX: H(a) = H_0 \sqrt{\Omega_r a^{-4} + \Omega_m a^{-3} + \Omega_k a^{-2} + \Omega_\Lambda}.$

Der Vergleich von Weltalter beziehungsweise Hubble-Zeit mit unabhängigen Altersbestimmungen von Himmelsobjekten wie Sternen und Kugelsternhaufen war immer wieder wichtig in der kritischen Bewertung von Messungen der Hubblekonstante und der anderen kosmologischen Parameter: das sich ergebende Weltalter muss größer als das der einzelnen Objekte sein, sonst ergeben die Messwerte keinen Sinn.

Geschichte

Die ersten Überlegungen zur Hubble-Konstante stammen von dem belgischen Priester und Physiker Georges Lemaître, der bereits 1927 in den „Annales de la Société scientifique de Bruxelles“ einen Aufsatz schrieb und die Konstante ermittelte zu

$LaTeX: H_0 \approx 625 \ \frac{\mathrm{km}}{\mathrm{s \cdot Mpc}}.$

Nach weiteren Hinweisen unter anderem von Carl Wilhelm Wirtz war es eine Arbeit von Edwin Hubble aus dem Jahr 1929, die einen linearen Zusammenhang zwischen Rotverschiebung und Entfernung von Galaxien behauptete. Hubble ermittelte für die Proportionalitätskonstante einen Wert von

$LaTeX: H_0 \approx 500 \ \frac{\mathrm{km}}{\mathrm{s \cdot Mpc}}.$

Das entsprechend geringe Weltalter von nur etwa zwei Milliarden Jahren wurde schon bald als problematisch im Vergleich zu Altersbestimmungen von Gesteinen angesehen.

Zu einer ersten deutlichen Korrektur nach unten kam es in den 1950ern nach der Entdeckung verschiedener Sternpopulationen durch Walter Baade. In Unkenntnis dieser Tatsache hatte Hubble in seinen früheren Arbeiten zu geringe Helligkeiten für die Cepheiden angenommen, die er zur Entfernungsbestimmung benutzte.

Weitere Verbesserungen ergaben bald Werte von

$LaTeX: H_0 \le 100 \ \frac{\mathrm{km}}{\mathrm{s \cdot Mpc}}.$

Die komplexen mehrstufigen Messverfahren führten zu einer langen und intensiv geführten Debatte von den 1970er bis zu den 1990er Jahren um den genauen Wert der Hubble-Konstante. Eine Gruppe um Allan Sandage und Gustav Tammann schlug Werte um 50 km s⁻¹ Mpc⁻¹ vor, während Astronomen wie Gerard de Vaucouleurs und Sidney van den Bergh höhere Werte um 100 km s⁻¹ Mpc⁻¹ bevorzugten. In dieser Zeit bürgerte es sich ein, die Hubble-Konstante als

$LaTeX: \Leftrightarrow H_0 = h \cdot 100 \ \frac{\mathrm{km}}{\mathrm{s \cdot Mpc}}$ mit $LaTeX: h \le 1$

zu beschreiben und die Abhängigkeit weiterführender kosmologischer Berechnungen vom genauen Wert der Hubble-Konstante durch ausdrückliche Angabe ihrer Abhängigkeit vom Faktor h zu verdeutlichen.

Nach den Ergebnissen des „H₀ Key Project“ mit dem Hubble-Weltraumteleskop ergab sich die Hubble-Konstante aus der Kombination von vier verschiedenen Methoden zu:

$LaTeX: H_0 \approx (72 \pm 8) \ \frac{\mathrm{km}}{\mathrm{s \cdot Mpc}}.$

Aus drei Jahren Messungen mit der Raumsonde WMAP (WMAP3) und Daten der 2dFGRS ergab sich als Wert:

$LaTeX: H_0 \approx (73 \pm 3) \ \frac{\mathrm{km}}{\mathrm{s \cdot Mpc}}.$

Einstein und Straus fanden, dass die kosmologische Expansion nur auf größten Skalen stattfinden kann. Die kosmologische Expansion von gravitativ gebundenen Objekten wie Sternen oder Galaxien ist dadurch ausgeschlossen. Eine Anzahl von Arbeiten und Messergebnissen lassen die kosmologische Expansion jedoch auch in wesentlich kleineren Bereichen möglich erscheinen.

Siehe auch

• Hubble-Konstante - Artikel in der deutschen Wikipedia

Literatur

• Carl Wilhelm Wirtz: De Sitters Kosmologie und die Radialbewegungen der Spiralnebel. In: Astronomische Nachrichten. Band 222, 1924, S. 21.
• E. Hubble: A Relation Between Distance and Radial Velocity among Extra-Galactic Nebulae. In: Proceedings of the National Academy of Sciences. Band 15, Nr. 3, 1929, S. 168.
• Wendy Freedman u. a.: Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant. In: Astrophysical Journal. Band 553, 2001, S. 47.
•  David Spergel u. a.: Three‐Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Implications for Cosmology. In: The Astrophysical Journal Supplement Series. 170, Nr. 2, 2007, S. 377–408, arxiv:astro-ph/0603449, doi:10.1086/513700.
•  Massimiliano Bonamente, Marshall K. Joy, Samuel J. LaRoque, John E. Carlstrom, Erik D. Reese, Kyle S. Dawson: Determination of the Cosmic Distance Scale from Sunyaev‐Zel’dovich Effect and Chandra X‐Ray Measurements of High‐Redshift Galaxy Clusters. In: The Astrophysical Journal. 647, Nr. 1, 10. August 2006, S. 25–54, arxiv:astro-ph/0512349, doi:10.1086/505291.
• Dominik J. Schwarz: Streit um Hubbles Erbe. Spektrum der Wissenschaft 7/2018, S. 12–21.

Weblinks

• J. Huchra zur Geschichte der Hubblekonstante (englisch) (John Huchra)
• Die Expansion des Universums steckt in einer Krise