Unsere alten Seiten bleiben vorerst hier online, werden aber nicht mehr gepflegt! Das neue AnthroWiki finden Sie wie gewohnt unter anthrowiki.at. |
| Eine freie Initiative von Menschen bei anthro.wiki, anthro.world und biodyn.wiki mit online Lesekreisen, Übungsgruppen, Vorträgen ... |
| |
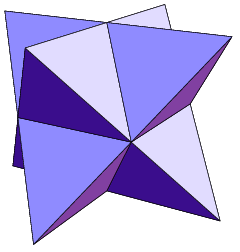
Sterntetraeder
Das Sterntetraeder, auch bekannt als Sternkörper zum Oktaeder, als Stella Octangula und als Keplerstern, ist ein achtstrahliger Stern und gehört zu den nicht-konvexen Deltaedern. Es handelt sich um einen vielflächigen Körper, der durch Verschmelzung zweier punktsymmetrischer Tetraeder entsteht. Das Sterntetraeder ist kein Sternkörper, weil nicht in allen Ecken gleich viele Flächen zusammentreffen.
Benannt durch Johannes Kepler im Jahr 1609, ist dies sowohl das einfachste reguläre zusammengesetzte Polyeder als auch das einfachste nicht-konvexe gleichmäßige Polyeder. Erstmals dargestellt wurde er durch Leonardo da Vinci in Luca Paciolis De Divina Proportione 1509.
Der Grafiker M. C. Escher hat das Sterntetraeder als Motiv für das Bild Doppelplanetoid verwendet: Das eine Tetraeder hat die Form einer von Menschen bewohnten Burg, während das andere eine mit dem ersten durchdrungene, von Dinosauriern bewohnte Welt darstellt.[1]
Inhaltsverzeichnis
[Verbergen]Eigenschaften
Die äußeren Eckpunkte des Körpers beschreiben einen Würfel, während die Schnittmenge der beiden Tetraeder ein Oktaeder darstellt, dessen Kanten wiederum die Innenkanten des Sterntetraeders darstellen.
Das Sterntetraeder ist die erste Stufe der konvexen Form des Sierpinski-Oktaeders.[2] Aus den acht kleinen Tetraedern können wieder Sterntetraeder gemacht werden, und dieser Vorgang kann wiederholt werden, so dass schließlich ein Fraktal entsteht, welches sich der Form eines Hexaeders annähert.[3][4]
Das Sterntetraeder kann als dreidimensionales Hexagramm angesehen werden: Das Hexagramm ist eine zweidimensionale Figur, die aus zwei überlappenden gleichseitigen Dreiecken gebildet wird, die punktsymmetrisch zueinander sind. Auf ähnliche Weise kann das Sterntetraeder aus zwei punktsymmetrisch überlappenden regelmäßigen Tetraedern gebildet werden. Dies kann auf höhere Dimensionen verallgemeinert werden. Die vierdimensionale äquivalente Konstruktion ist die Verbindung von zwei Pentachorons.
Das Sterntetraeder kann auch als Iterationsschritt beim Erzeugen einer dreidimensionalen „Koch-Kurve“ angesehen werden. Das ist ein Fraktals, das durch wiederholtes Hinzufügen kleinerer Tetraeder an jeder dreieckigen Fläche einer größeren Figur gebildet wird. Der Iterationsschritt 0 der dreidimensionalen „Koch-Kurve“ ist ein einzelnes Tetraeder, und der Iterationsschritt 1, der durch Hinzufügen von vier kleineren Tetraedern an die Flächen des zentralen Tetraeders gebildet wird, ist das Sterntetraeder.
Formeln

| Größen eines Sterntetraeders mit Kantenlänge a bzw. b = a/2 | ||
|---|---|---|
| Volumen |
| |
| Oberflächeninhalt | ||
| Umkugelradius | ||
| Kantenkugelradius | ||
| Inkugelradius | ||
| Raumdiagonale | ||
| Kantenabstand | ||
| Verhältnis von Volumen zu Umkugelvolumen | ||
| Innenwinkel des gleichseitigen Dreiecks | ||
| Winkel zwischen benachbarten Flächen | ||
| Winkel zwischen Kante und Fläche | ||
| Tetraederwinkel | ||
| Raumwinkel in den Ecken | ||
| Sphärizität | ||
- Das Volumen des Sterntetraeders ist gleich der Summe der Volumina von einem Oktaeder und 8 aufgesetzten Tetraedern mit jeweils halber Kantenlänge
. Es füllt den umgrenzenden Würfel mit dem Volumen
zur Hälfte aus.
- Der Umkugelradius des Sterntetraeders entspricht dem eines einzelnen Tetraeders.
Anwendung in der Kunst
Siehe auch
- Sterntetraeder - Artikel in der deutschen Wikipedia
Weblinks
- Eric W. Weisstein: Sterntetraeder. In: MathWorld (englisch).
- Stellated Octahedron Calculator (Web Application zum Berechnen)
Einzelnachweise
- Hochspringen ↑ M. C. Escher: Double Planetoid.
- Hochspringen ↑ Keplerian Fractals (Memento vom 16. März 2015 im Internet Archive)
- Hochspringen ↑ Approaching a Fractal Cube by a series of non-convex polyhedra
- Hochspringen ↑ Keplerian Fractals
| Dieser Artikel basiert (teilweise) auf dem Artikel Sterntetraeder aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons Attribution/Share Alike. In Wikipedia ist eine Liste der Autoren verfügbar. |