Kugel

Bild einer Kugel mit Längen- und Breitenkreisen

Kugelschale, rechts: aufgeschnitten

Der blaue Körper ist ein Kugelsegment und ebenso der rosa Restkörper.

Eine Kugel (griech. σφαίρα sphaira „Sphäre“) ist in der Geometrie die Kurzbezeichnung für Kugelfläche und Kugelkörper. Die Differenzmenge zweier konzentrischer Kugeln bildet eine Kugelschale bzw. Hohlkugel. Durch den Schnitt mit einer Ebene ensteht ein Kugelabschnitt bzw. Kugelsegment, dessen gewöbter Teil auch als Kugelkalotte, Kugelhaube oder Kugelkappe bezeichnet wird und desen Grundfläche eine Kreisscheibe ist. Der Schnitt durch einen Großkreis teilt die Kugel in zwei Halbkugeln oder Hemisphären (von griech. ἡμισφαίριον hemisphairion „Halbkugel“).

Einheitskugel

Eine Kugel mit dem Radius eins um den Nullpunkt eines Vektorraums wird als Einheitskugel bezeichnet.

Kugelfläche und Kugelkörper

Die Kugelfläche ist die bei der Drehung einer Kreislinie um einen Kreisdurchmesser entstehende Fläche. Sie ist eine Rotationsfläche sowie eine spezielle Fläche zweiter Ordnung und wird beschrieben als die Menge (der geometrische Ort) aller Punkte im dreidimensionalen euklidischen Raum, deren Abstand von einem festen Punkt des Raumes gleich einer gegebenen positiven reellen Zahl $LaTeX: \!\ r$ ist. Der feste Punkt wird als Mittelpunkt oder Zentrum der Kugel bezeichnet, die Zahl $LaTeX: \!\ r$ als Radius der Kugel.

Die Kugelfläche teilt den Raum in zwei getrennte offene Untermengen, von denen genau eine konvex ist. Diese Menge heißt das Innere der Kugel. Die Vereinigungsmenge einer Kugelfläche und ihres Inneren heißt Kugelkörper oder Vollkugel. Die Kugelfläche wird auch Kugeloberfläche oder Sphäre genannt.

Sowohl Kugelfläche als auch Kugelkörper werden oft kurz als Kugel bezeichnet, wobei aus dem Zusammenhang klar sein muss, welche der beiden Bedeutungen gemeint ist.

Eine Kugelfläche mit Mittelpunkt ($LaTeX: \!\ x_0$, $LaTeX: \!\ y_0$, $LaTeX: \!\ z_0$) und Radius $LaTeX: \!\ r$ ist die Menge aller Punkte ($LaTeX: \!\ x$, $LaTeX: \!\ y$, $LaTeX: \!\ z$), für die

$LaTeX: \!\ (x - x_0)^2 + (y - y_0)^2 + (z - z_0)^2 = r^2$

erfüllt ist.

Kugelkoordinaten und kartesisches Koordinatensystem

In Vektorschreibweise mit $LaTeX: \vec{x} = \begin{pmatrix}x \\ y \\ z\end{pmatrix}$, $LaTeX: \vec{m} = \begin{pmatrix}x_0 \\ y_0 \\ z_0\end{pmatrix}$:

$LaTeX: (\vec x - \vec m ) \cdot (\vec x - \vec m ) = r^2$,

$LaTeX: (\vec x - \vec m )^2 = r^2$,

$LaTeX: |\vec x - \vec m |^2 = r^2$ oder

$LaTeX: |\vec x - \vec m | = r$.

Die Punkte auf der Kugelfläche mit dem Radius $LaTeX: \!\ r$ und dem Zentrum im Ursprung können durch Kugelkoordinaten wie folgt parametrisiert werden:

$LaTeX: x = r \cdot \sin \theta \cdot \cos \varphi$

$LaTeX: y = r \cdot \sin \theta \cdot \sin \varphi$

$LaTeX: z = r \cdot \cos \theta$

mit $LaTeX: 0 \le \theta \le \pi$ und $LaTeX: 0 \le \varphi < 2 \pi$.

Großkreise und Kleinkreise

Ein Kreis auf der Oberfläche der Kugel, dessen Mittelpunkt mit dem Mittelpunkt der Kugel zusammenfällt, ist ein größtmöglicher Kreis auf der Kugelfläche und wird als Großkreis bezeichnet. Sein Radius ist gleich dem der Kugel. Solche Großkreise sind etwa die in Nord-Süd-Richtung verlaufenden und durch die beiden Rotationspole der Erde gehenden Längenkreise auf der kugelförmig gedachten Erdoberfläche.

Alle anderen Kreise auf der Kugeloberfläche werden als Kleinkreise bezeichnet. Ein Beispiel dafür sind die senkrecht zur Erdachse stehenden Breitenkreise, ausgenommen der Äquator, dessen Mittelpunkt mit dem Mittelpunkt der Erde zusammenfällt und daher ein Großkreis ist.

Formeln

Formelsammlung Geometrie - Artikel in der deutschen Wikipedia

Formeln zur Kugel

Geometrische Größe	Formel
Kugelradius	$LaTeX: \!\ r$
Kugeldurchmesser	$LaTeX: \!\ d =2 r$
Umfang (Großkreis)	$LaTeX: U =2 \pi r = \pi d\ {\color{OliveGreen} = \frac{\mathrm dA_\mathrm{PF}}{\mathrm dr}}$
Volumen	$LaTeX: V = \frac{4}{3} \pi r^3 = \frac{1}{6} \pi d^3 = \int_{-r}^r \left(r^2-x^2\right)\pi \mathrm dx$
Oberfläche	$LaTeX: A_O = 4 \pi r^2 = \pi d^2\ {\color{OliveGreen} = \frac{\mathrm dV}{\mathrm dr}}$
Projektionsfläche/Kugelquerschnitt	$LaTeX: A_\mathrm{PF} = \pi r^2 = \int_0^r U \mathrm dr$
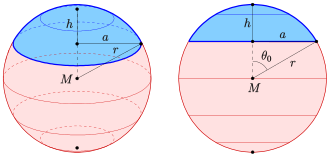
Höhe (Kugelsegment/-kalotte, Kugelschicht, nicht mit dem h in der Skizze unten identisch)	$LaTeX: \!\ h$
Volumen einer Kugelkalotte	$LaTeX: V_\mathrm{KK} = \frac{\pi h^2}{3} (3r - h)$
Flächeninhalt einer Kugelkalotte	$LaTeX: A_\mathrm{KK} = 2 \pi r h = 2 \pi r^2 \left(1-\cos\frac{\alpha}{2}\right)$
Mantelfläche einer Kugelschicht	$LaTeX: A_\mathrm{KS} = 2 \pi r h = 2 \pi r^2 \int_\alpha^\beta \sin x\,\mathrm dx$
Trägheitsmoment einer Hohlkugel (Drehachse durch Mittelpunkt)	$LaTeX: J = \frac{2}{3} mr^2$
Trägheitsmoment einer Vollkugel (Drehachse durch Mittelpunkt)	$LaTeX: J = \frac{2}{5} mr^2$

Zu etlichen weiteren Unterthemen siehe auch

• Kugel - Artikel in der deutschen Wikipedia

Siehe auch

• Kugel - Artikel in der deutschen Wikipedia