Unsere alten Seiten bleiben vorerst hier online, werden aber nicht mehr gepflegt! Das neue AnthroWiki finden Sie wie gewohnt unter anthrowiki.at. |
| Eine freie Initiative von Menschen bei anthro.wiki, anthro.world und biodyn.wiki mit online Lesekreisen, Übungsgruppen, Vorträgen ... |
| |
Raum (Mathematik)
Ein Raum ist in der Mathematik als abstrakte Verallgemeinerung des uns gewohnten Anschauungsraums als eine Menge mathematischer Objekte mit einer mathematischen Struktur definiert, z.B. als Vektorraum oder als topologischer Raum bzw. als Mannigfaltigkeit. Auf die Anschaulichkeit wird dabei verzichtet.
Inhaltsverzeichnis
[Verbergen]Vektorraum
Ein -dimensionaler Vektorraum
besteht aus einer Menge von mathematischen Objekten, die Vektoren (von lat. vector „Träger, Fahrer“) genannt werden und addiert, subtrahiert oder mit einem Skalar (z.B. einer Zahl) multipliziert werden können, sodass der daraus resultierende Vektor wiederum ein Element desselben Vektorraums ist und die Assoziativgesetze und Distributivgesetze erfüllt sind. Einen Vektorraum, dessen Elemente als Funktionen betrachtet werden, bezeichnet man als Funktionenraum.
Die Vektoren werden geometrisch-symbolisch in der Regel als Pfeile mit bestimmter Länge und Richtung dargestellt. Als mathematische Objekte können dafür beispielsweise reelle oder komplexe Zahlen, Zahlentupel, Matrizen oder Funktionen verwendet werden. Die Skalare entstammen einem bestimmten Körper, z.B. dem Körper der reellen Zahlen oder dem Körper
der komplexen Zahlen, weshalb ein Vektorraum stets über einem bestimmten Körper definiert ist. Im gegebenen Fall handelt es sich dann beispielsweise um einen reellen oder komplexen Vektorraum.
Als Ortsvektor (auch Radiusvektor oder Positionsvektor) eines Punktes wird ein Vektor
bezeichnet, der von einem festgelegten Punkt
(meist dem Ursprung des Koordinatensystems) zu diesem Punkt zeigt.
Basis
Die Basis eines Vektorraums wird durch eine Menge von Basisvektoren gebildet, durch als deren endliche Linearkombination sich jeder Vektor des Raumes eindeutig darstellen lässt. Bei einem Funktionenraum bezeichnet man sie auch als Basisfunktionen. Die Standardbasis des Vektorraums ist beispielsweise die Menge der kanonischen Einheitsvektoren
. Für den Vektorraum der Polynome über einem Körper wird meist die Basis
verwendet.
Im Allgemeinen kann ein Vektorraum über verschiedene Basen verfügen. Der Übergang von einer Basis zu einer Basis
wird durch einen Basiswechsel bzw. durch eine Basistransformation vollzogen, die eine identische Abbildung
des Vektorraums auf sich selbst ist. Sie kann mithilfe einer Transformationsmatrix (auch Basiswechselmatrix oder Übergangsmatrix)
beschrieben werden. Dabei handelt es sich um den Spezialfall einer Abbildungsmatrix (auch Darstellungsmatrix)
, durch die ganz allgemein lineare Abbildungen zwischen zwei beliebig dimensionalen Verktorräumen
und
dargestellt werden. Für eine Basistransformation ist daher
Die Koeffizienten der Transformationsmatrix ergeben sich, indem man die Basisvektoren
der ursprünglichen Basis
als Linearkombination der Basisvektoren
der neuen Basis
darstellt, d.h.:
Dualraum
Der Dualraum eines Vektorraums über einem Körper
ist der Vektorraum aller linearen Abbildungen von
nach
. Diese linearen Abbildungen werden manchmal auch Kovektoren genannt.
Vektorrechnung
In der Vektorrechnung sind verschiedene Rechenoperationen für Vektoren definiert. Die Vektoren können dazu als Spaltenvektor oder in Komponentenschreibweise angeschrieben werden. Die wichtigsten Rechenoperationen zeigt die nachstehende Tabelle:
| Rechenoperation | Spaltenvektoren | Komponentenschreibweise | Beschreibung |
|---|---|---|---|
| Addition/Subtraktion | |||
| Multiplikation mit einem Skalar | |||
| Skalarprodukt | |||
| Betrag | Der Betrag gibt die Länge des Vektors an. | ||
| Kreuzprodukt (Vektorprodukt) |
|
Der Betrag des Vektorprodukts entspricht der Fläche des von den beiden Vektoren aufgespannten Parallelogramms:
| |
| Spatprodukt | Der Betrag des Spatprodukts entspricht dem Volumen des von den drei Vektoren aufgespannten Parallelepipeds:
| ||
| Dyadisches Produkt (tensorielles Produkt) |
Siehe auch
- Raum (Mathematik) - Artikel in der deutschen Wikipedia
- Vektor - Artikel in der deutschen Wikipedia
Literatur
- Tilo Arens, Frank Hettlich, Christian Karpfinger, Ulrich Kockelkorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik, 4. Auflage, Springer Spektrum 2018, ISBN 978-3662567401, eBook ISBN 978-3-662-56741-8
Einzelnachweise
- Hochspringen ↑ nach dem Satz von Pythagoras
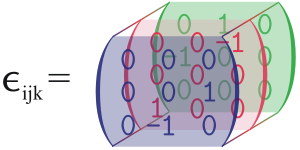
- Hochspringen ↑
ist das Levi-Civita-Symbol und ist +1 für gerade Permutationen von (1, 2, 3), −1 für ungerade Permutationen und sonst 0.
| Dieser Artikel basiert (teilweise) auf dem Artikel Raum (Mathematik) aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons Attribution/Share Alike. In Wikipedia ist eine Liste der Autoren verfügbar. |



