Unsere alten Seiten bleiben vorerst hier online, werden aber nicht mehr gepflegt! Das neue AnthroWiki finden Sie wie gewohnt unter anthrowiki.at. |
| Eine freie Initiative von Menschen bei anthro.wiki, anthro.world und biodyn.wiki mit online Lesekreisen, Übungsgruppen, Vorträgen ... |
 Wie Sie die Entwicklung von AnthroWiki durch Ihre Spende unterstützen können, erfahren Sie hier.
|
Dodekaeder: Unterschied zwischen den Versionen
(→Siehe auch) |
(→Das regelmäßige Pentagondodekaeder) |
||
| Zeile 11: | Zeile 11: | ||
== Das regelmäßige Pentagondodekaeder == | == Das regelmäßige Pentagondodekaeder == | ||
| − | Wegen seiner hohen [[ | + | Wegen seiner hohen [[Symmetrie (Geometrie)|Symmetrie]] – alle Ecken, Kanten und Flächen sind untereinander gleichartig – ist das Dodekaeder ein ''reguläres [[Polyeder]]''. Es hat: |
* sechs fünfzählige Drehachsen (durch gegenüberliegende Flächenmittelpunkte) | * sechs fünfzählige Drehachsen (durch gegenüberliegende Flächenmittelpunkte) | ||
* zehn dreizählige Drehachsen (durch gegenüberliegende Ecken) | * zehn dreizählige Drehachsen (durch gegenüberliegende Ecken) | ||
| Zeile 18: | Zeile 18: | ||
und ist | und ist | ||
* inversionssymmetrisch (Punktspiegelung bezüglich des Dodekaedermittelpunkts) | * inversionssymmetrisch (Punktspiegelung bezüglich des Dodekaedermittelpunkts) | ||
| − | Insgesamt hat die Symmetriegruppe des Dodekaeders – die ''Dodekaeder-'' oder ''[[ | + | Insgesamt hat die Symmetriegruppe des Dodekaeders – die ''Dodekaeder-'' oder ''[[Ikosaedergruppe]]'' – 120 Elemente. Die 60 [[Orientierung (Mathematik)|orientierungserhaltenden]] Symmetrien entsprechen der [[Wikipedia:Alternierende Gruppe|alternierenden Gruppe]] <math>A_5</math>. Manchmal wird auch diese Untergruppe „Ikosaedergruppe“ genannt. Die volle Symmetriegruppe ist isomorph zu dem direkten Produkt <math>A_5 \times C_2</math>. Dass das Produkt direkt ist, sieht man daran, dass die Punktspiegelung am Mittelpunkt mit den Drehungen kommutiert. |
| − | Die Symmetrie des Dodekaeders ist durch die hier auftretenden fünfzähligen Symmetrieachsen mit einer periodischen Raumstruktur nicht verträglich (siehe [[Wikipedia:Parkettierung|Parkettierung]]). Es kann daher kein [[ | + | Die Symmetrie des Dodekaeders ist durch die hier auftretenden fünfzähligen Symmetrieachsen mit einer periodischen Raumstruktur nicht verträglich (siehe [[Wikipedia:Parkettierung|Parkettierung]]). Es kann daher kein [[Kristallgitter]] mit Ikosaedersymmetrie geben (vgl. jedoch [[Wikipedia:Quasikristall|Quasikristall]]e). |
== Zu etlichen weiteren Themen siehe auch == | == Zu etlichen weiteren Themen siehe auch == | ||
Version vom 13. Februar 2020, 07:47 Uhr
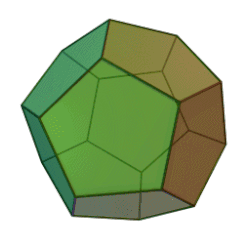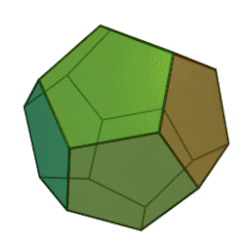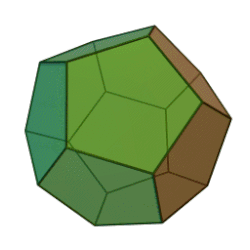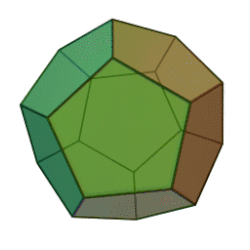
Das Dodekaeder [ˌdodekaˈʔeːdər] (von griech. Zwölfflächner; dt. auch (das) Zwölfflach) ist ein Körper mit zwölf Flächen. In der Regel ist damit ein platonische Körper gemeint, nämlich das (regelmäßige) Pentagondodekaeder, ein Körper mit
- 12 (kongruenten) regelmäßigen Fünfecken als Flächen
- 20 Ecken, in denen jeweils drei dieser Fünfecke zusammentreffen
- 30 (gleich langen) Kanten, von denen jede die Seite von zwei Fünfecken ist.
Es gibt aber auch andere Dodekaeder von hoher Symmetrie.
Das regelmäßige Pentagondodekaeder
Wegen seiner hohen Symmetrie – alle Ecken, Kanten und Flächen sind untereinander gleichartig – ist das Dodekaeder ein reguläres Polyeder. Es hat:
- sechs fünfzählige Drehachsen (durch gegenüberliegende Flächenmittelpunkte)
- zehn dreizählige Drehachsen (durch gegenüberliegende Ecken)
- fünfzehn zweizählige Drehachsen (durch die Mittelpunkte gegenüberliegender Kanten)
- fünfzehn Symmetrieebenen (durch einander gegenüberliegende – und parallele – Kanten)
und ist
- inversionssymmetrisch (Punktspiegelung bezüglich des Dodekaedermittelpunkts)
Insgesamt hat die Symmetriegruppe des Dodekaeders – die Dodekaeder- oder Ikosaedergruppe – 120 Elemente. Die 60 orientierungserhaltenden Symmetrien entsprechen der alternierenden Gruppe . Manchmal wird auch diese Untergruppe „Ikosaedergruppe“ genannt. Die volle Symmetriegruppe ist isomorph zu dem direkten Produkt
. Dass das Produkt direkt ist, sieht man daran, dass die Punktspiegelung am Mittelpunkt mit den Drehungen kommutiert.
Die Symmetrie des Dodekaeders ist durch die hier auftretenden fünfzähligen Symmetrieachsen mit einer periodischen Raumstruktur nicht verträglich (siehe Parkettierung). Es kann daher kein Kristallgitter mit Ikosaedersymmetrie geben (vgl. jedoch Quasikristalle).
Zu etlichen weiteren Themen siehe auch
- Dodekaeder - Artikel in der deutschen Wikipedia
Siehe auch
- Dodekaeder - Artikel in der deutschen Wikipedia
| Dieser Artikel basiert (teilweise) auf dem Artikel Dodekaeder aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons Attribution/Share Alike. In Wikipedia ist eine Liste der Autoren verfügbar. |
