Funktion (Mathematik)

Graphen einiger Potenzfunktionen

Polynomfunktion mit mehreren Nullstellen

Graph der Funktion $LaTeX: f(x,y) = \sin\left(x^2\right)\cos\left(y^2\right)$

Kubische Kurve mit einem einfachen Doppelpunkt bei (0,0): y² = x²(x + 1)

Die Normalparabel $LaTeX: f(x) = x^2$ ist eine gerade Funktion.

Die kubische Funktion $LaTeX: f(x) = x^3$ ist eine ungerade Funktion.

Als Funktion (von lat. functio „Tätigkeit, Verrichtung“) oder Abbildung wird in der Mathematik eine Relation zwischen zwei Mengen bezeichnet, bei der jedem Element der Definitionsmenge $LaTeX: D$ (Funktionsargument, unabhängige Variable, $LaTeX: x$-Wert) genau ein Element der Zielmenge bzw. des Wertevorrats $LaTeX: Z$ (Funktionswert, abhängige Variable, $LaTeX: y$-Wert bzw. $LaTeX: f(x)$) zugeordnet wird:

$LaTeX: f\colon\, D\to Z,\; x\mapsto y$,   oder äquivalent:   $LaTeX: f\colon\, \begin{cases} D\to Z \\ x\mapsto y\end{cases}$

Eine Selbstabbildung ist eine Abbildung, die eine Menge $LaTeX: M$ auf sich selbst abbildet: $LaTeX: \alpha\colon M \to M$. Einfache Beispiele dafür sind etwa das Zählen oder die identische Abbildung.

Grundlagen

Eine Funktion kann etwa durch eine Funktionsgleichung mit zugehöriger Definitionsmenge oder durch eine eindeutige Zuordnungsvorschrift angegeben werden, z.B.:

$LaTeX: f(x) = x^2, \qquad x \in \mathbb{N}$

oder

$LaTeX: x \mapsto x^2, \qquad x \in \mathbb{N}$

Ein Element $LaTeX: x_0$ der Definitionsmenge heißt Nullstelle, wenn gilt: $LaTeX: f\left(x_0\right)=0$.

Der Funktionsbegriff lässt sich auf eine beliebige Anzahl von Variablen erweitern. Die Definitionsmenge besteht dann aus n-Tupeln von Zahlen. Die nebenstehende Abbildung veranschaulicht beispielsweise eine Funktion mit zwei Variablen:

$LaTeX: f(x,y) = \sin\left(x^2\right)\cos\left(y^2\right)$

Funktionsgraph

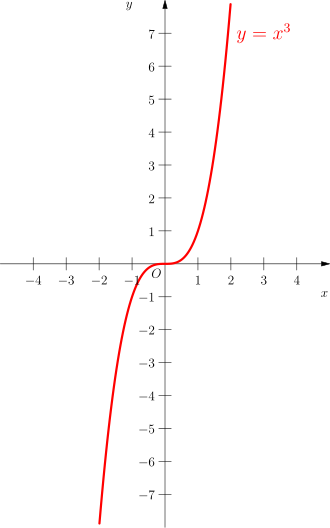
Die Menge der geordneten Paare $LaTeX: (x, f(x))$ bildet den Funktionsgraph (kurz: Graph), der graphisch in einem zweidimensionalen Koordinatensystem veranschaulicht werden kann, wobei auf der horizontalen $LaTeX: x$-Achse die Funktionsargumente und auf der $LaTeX: y$-Achse die zugehörigen Funktionswerte eingezeichnet sind. Die Grafik rechts oben zeigt etwa die Funktionsgraphen einiger Potenzfunktionen:

$LaTeX: f\colon x \mapsto a x^r \qquad a,x,r \in \mathbb{R}$

Bild

Gegeben sei eine Funktion $LaTeX: f\colon\, D\to Z$ und eine Teilmenge $LaTeX: M \subseteq D$ (dabei kann es sich auch um ein einzelnes Element $LaTeX: x \in D$ handeln) der Definitionsmenge; dann ist das Bild (auch Bildmenge oder Bildbereich von $LaTeX: M$ unter $LaTeX: f$ wie folgt definiert:

$LaTeX: f(M) := \{ f(x) \mid x \in M\}$  das Bild von $LaTeX: M$ unter $LaTeX: f$.

Das Bild der gesamten Definitionsmenge $LaTeX: D$ ist folglich:

$LaTeX: \operatorname{Bild}(f) := f(D)$

Urbild

Gegeben sei wieder eine Funktion $LaTeX: f\colon\, D\to Z$ und eine Teilmenge $LaTeX: M \subseteq Z$ der Zielmenge; dann ist das Urbild von $LaTeX: M$ unter $LaTeX: f$ gegeben durch:

$LaTeX: f^{-1}(M) := \left\{x\in A\mid f(x)\in M\right\}$

Diese Urbildfunktion weist jedem Element $LaTeX: M$ der Potenzmenge $LaTeX: \mathcal{P}(Z)$ der Zielmenge $LaTeX: Z$ (d.h. der Menge all ihrer Teilmengen) das Urbild $LaTeX: f^{-1}(M)$ als Element der Potenzmenge $LaTeX: \mathcal{P}(D)$ der Definitionsmenge $LaTeX: D$ zu.

Identische Abbildung

Eine Funktion über einer Menge $LaTeX: M$, die genau ihr Argument zurückgibt, ist eine identische Abbildung:

$LaTeX: \operatorname{id}_M(x) = x$

Umkehrfunktion

Die Umkehrfunktion oder inverse Funktion $LaTeX: f^{-1}\colon B \to A$ einer bijektiven Funktion $LaTeX: f\colon A \to B$ weist jedem Element der Zielmenge $LaTeX: B$ sein eindeutig bestimmtes Urbildelement der Definitionsmenge $LaTeX: A$ zu.

Fixelement

Ein Fixelement $LaTeX: x$ ist ganz allgemein ein Element der Definitionsmenge $LaTeX: X$, das durch eine gegebene Abbildung $LaTeX: f \colon X \to X$ auf sich selbst abgebildet wird, dass also für $LaTeX: x \in X$ gilt:

$LaTeX: f(x) = x$

Ein Punkt, der auf sich selbst abgebildet wird, heißt Fixpunkt. Eine Gerade, die auf sich selbst abgebildet wird, nennt man Fixgerade. Bei dieser muss es sich nicht notwendigerweise um eine Fixpunktgerade handeln, bei der zugleich auch alle Punkte auf sich selbst abgebildet werden, diese also Fixpunkte sind. Analog verhält es sich bei einer Fixebene oder Fixpunktebene, wie sie etwa bei einer Ebenenspiegelung auftreten. Das Prinzip läss sich auf Räume beliegbiger Dimensionen erweitern. Man spricht dann ganz allgemein von einem Fixraum.

Gerade und ungerade Funktionen

Eine gerade Funktion ist eine reelle Funktion in einer Variablen, deren Funktionsgraph achsensymmetrisch zur y-Achse ist. Eine ungerade Funktion zeichnet sich hingegen dadurch aus, dass der Funktiongraph punktsymmetrisch zum Koordinatenursprung ist.

Symmetrische und antisymmetrische Funktionen

Eine symmetrische Funktion ist eine Funktion mehrerer Variablen, bei der die Variablen untereinander vertauscht werden können, ohne dass sich der Funktionswert verändert. Eine antisymmetrische Funktion ändert hingegen bei der Vertauschung zweier Variablen das Vorzeichen. Für zwei Variable gilt also beispielsweise:

$LaTeX: f(x,y) = \quad f(y,x) \qquad symmetrisch$

$LaTeX: f(x,y) = - f(y,x) \qquad antisymmetrisch$

In der Quantenphysik sind beispielsweise die Wellenfunktionen der Bosonen symmetrisch bzgl. der Vertauschung der Teilchenpositionen, die der Fermionen hingegen antisymmetrisch, woraus das Pauli-Prinzip folgt, das den schalenförmigen Aufbau der Elektronenhülle der Atome erklärt.

Glatte Funktion

Eine glatte Funktion ist stetig und unendlich oft differenzierbar.

Konstante Funktion

Eine konstante Funktion (von lat. constans „feststehend“) nimmt für alle Argumente stets denselben Funktionswert an, d.h. eine Funktion $LaTeX: f$ ist genau dann konstant, wenn für alle $LaTeX: x,y \in A$ gilt: $LaTeX: f(x)=f(y)$.

Lineare Funktion

Eine lineare Funktion enthält die Unbekannte(n) nur in der ersten Potenz; in ihrer einfachsten Form lautet daher ihre Funktionsgleichung mit den konstanten Parametern $LaTeX: a, b$:

$LaTeX: f(x) = a \cdot x + b$

Ihr Funktionsgraph ist eine Gerade, deren Steigung gleich $LaTeX: a$ ist.

Indikatorfunktion

Eine Indikatorfunktion oder charakteristische Funktion kann nur nur ein oder zwei Funktionswerte annehmen. Damit können komplexe Menge mathematisch exakt erfasst werden. Ein Beispiel ist die nach dem deutschen Mathematiker Peter Gustav Lejeune Dirichlet benannte Dirichlet-Funktion, die die charakteristische Funktion der rationalen Zahlen ist:

$LaTeX: D\colon \mathbb R\to\mathbb R,\quad x\mapsto D(x)=\begin{cases} 1, & \mbox{wenn }x\mbox{ rational,} \\ 0, & \mbox{wenn }x\mbox{ irrational.} \end{cases}$

Komplexwertige Funktion

Eine komplexwertige Funktion hat eine Zielmenge $LaTeX: Z$ aus dem Bereich der komplexen Zahlen $LaTeX: \mathbb C$, wobei die Definitionsmenge $LaTeX: D$ nicht allgemein festgelegt ist und beispielsweise auch auf den Bereich der reellen Zahlen eingeschränkt sein kann. Das ist etwa bei der Eulerschen Formel der Fall:

$LaTeX: f(x) = \mathrm{e}^{\mathrm{i}\,x} = \cos\left(x \right) + \mathrm{i}\,\sin\left( x\right), \qquad x\in\mathbb R,\, f(x)\in\mathbb C$

Demgegenüber wird der Begriff komplexe Funktion nicht in eindeutiger Weise verwendet, sondern teilweise synonym zur komplexwertigen Funkton, teilweise so, dass auch die Definitionsmenge $LaTeX: D$ dem Bereich der komplexen Zahlen angehört.

Siehe auch

• Funktion (Mathematik) - Artikel in der deutschen Wikipedia